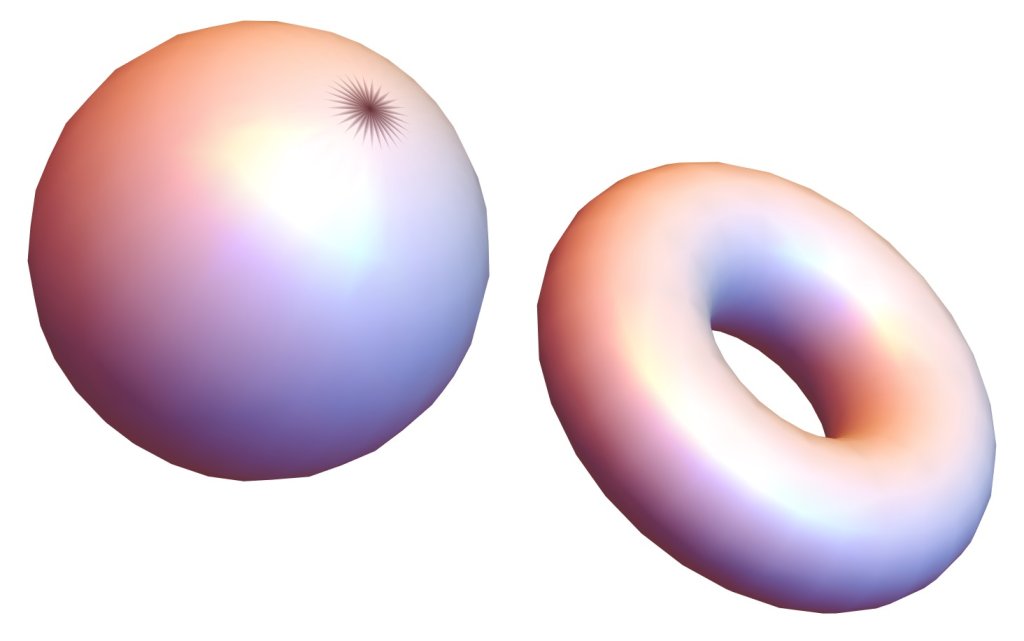A felfújási sejtés algebrai felületekre vonatkozó bizonyítása hozzájárulhat a fizikai elméletek – például a húrelmélet – jobb megértéséhez is.
Két magyar matematikus, Gyenge Ádám (BME Matematikai Intézet) és Szabó Szilárd (a kutatás idején BME, jelenleg ELTE Matematikai Intézet) jelentős áttörést ért el egy neves matematikai sejtés speciális esetének bizonyításával. Tanulmányukat a világ egyik legnevesebb szakfolyóirata, az Advances in Mathematics közli le.
A kutatók a matematikai fizika egyik kiemelkedő alakja, a Fields-érmes Makszim Koncevics által megfogalmazott, úgynevezett felfújási sejtés (blow-up conjecture) egyik részesetét bizonyították. Egy különleges matematikai szabályról van szó, amelyet eddig még a legegyszerűbb esetekre se sikerült bizonyítani. A két magyar matematikus sikeresen megoldott egy fontos részproblémát, amely így közelebb vihet a teljes kérdéskör megértéshez.
A felfújási sejtés az algebrai geometriához és azon belül a kvantumkohomológia nevű, modern matematikai területhez kapcsolódik, amely kapcsolatokat tár fel a geometriai terek és kvantumfizikai jelenségek között.
| Mi az a kohomológia? A kohomológia olyan módszer, amellyel egy geometriai tér alakját algebrai objektumok (például számok) segítségével derítjük fel. Dimenziónként invariánsokat rendel a térhez, amelyek a pontok, vonalszerű hurkok, felületszerű hézagok és magasabb dimenziós „lyukak” jelenlétét mérik. A kohomológia előnye, hogy egy felület vagy tér bonyolult geometriai tulajdonságait egyszerűbb, számolható algebrai adatokra redukálja. Például a gömb egydimenziós kohomológiája triviális, azaz 0 (nincs benne lyuk), míg az úszógumi alakú tórusz (lásd lent) egydimenziós kohomológiája nem triviális, azaz nem 0. A kvantumkohomológia a hagyományos kohomológiát ahhoz hasonlóan finomítja, mint a kvantummechanika a klasszikus fizikát. Részletesebb, finomabb képet ad egy-egy geometriai objektumról. |
„Ez egy nem túl régi, a kétezres években született sejtés, mi egy konferencián találkoztunk vele, még a Covid-járvány idején. Azért tetszett meg, mert bár az algebrai geometria különböző területeivel foglalkozunk, mindkettőnk területéhez közel áll. Meg persze azért is, mert egy igazi sztármatematikus, a számos rangos díjjal kitüntetett Makszim Koncevics dobta be” – mondta a bme.hu-nak Gyenge Ádám.
De mi is ez az egész?
Egy olyan geometriai műveletről van szó, amelyet a matematikusok „felfújásnak” hívnak. Képzeljünk el egy felületet, ahol egy kiválasztott pont környezete helyére egy másik apró felületdarabot illesztünk be – mintha a felületet megszúrnánk, és ott egy kis csavarodás jelenne meg, melynek pontjai megfeleltethetők az eredeti felület bizonyos pontjainak. A sejtés azt mondja ki, hogy egy ilyen módosítás után is megmarad a rend a rendszerben: a módosított alakzat viselkedése kiszámítható az eredeti alakzatéból.
A kvantumkohomológia olyan, mintha egy tér alakját és szerkezetét leíró klasszikus térképet kiegészítenénk apró, rejtett kvantumhatásokkal – mintha a tér emlékezne arra, hogyan lehet benne eljutni egyik pontból a másikba különféle görbék mentén. E kiegészített térkép új szabályokat hoz létre, ahol a geometriai összefüggések nemcsak a formákról, hanem az azokat átszövő, kvantumszintű útvonalakról is mesélnek.
Az ezen útvonalakat leíró kvantumkonnexió úgy viselkedik, mint egy láthatatlan térkép, amely megmutatja, hogyan változik egy geometriai tér belső szerkezete, ha benne mozogni kezdünk – mintha egy iránytű vezetne minket egy görbült világban. Ennek a rendszernek a spektruma pedig olyan, mint a tér rezonanciáinak listája: megmutatja, milyen sajátos módokon képes rezegni a tér, hasonlóan ahhoz, ahogy egy hangszer húrjai különböző hangokon szólalnak meg.
Koncevics sejtése azt állítja, hogy van egyfajta szabályosság az alaptér és annak felfújtja között: az új alakzat kvantumlenyomata (spektruma) levezethető az eredeti alakzat kvantumspektrumából.
Vagyis a bonyolult új geometria rejti az eredeti geometria információját, csak más formában.
Gyenge Ádám és Szabó Szilárd az algebrai felületekre – azaz kétdimenziós terekre – vonatkozóan igazolta a sejtést, és ez lehet az első lépés a teljes bizonyításhoz. Ami még így sem lesz könnyű, mert az alapeset bizonyítása is rendkívüli technikai nehézségekkel járt – jegyezte meg Gyenge Ádám. Több mint 2 évig dolgoztak vele, sőt a tanulmány bírálata is 2 évig tartott, ami nem gyakori, de azért előfordul a tudomány világában.
„A munka részben intuitív, de azért szisztematikus folyamat volt” – mondta kérdésünkre az Algebra és Geometria Tanszék docense. Hozzátette, volt már alkalmuk beszélni Konceviccsel, megmutatták neki az eredményt, és őt is meggyőzte. A tanulmány novemberben nyomtatásban is megjelenik.
Miért fontos ez?
A felfedezés nemcsak a magas szintű elméleti matematika számára mérföldkő, hanem megerősíti a kvantumtérelmélet és a modern geometria közötti kapcsolatokat is. Egy ilyen bizonyítás új eszközöket adhat más, jelenleg nyitott problémák megközelítéséhez, sőt hozzájárulhat a fizikai elméletek, például a húrelmélet jobb megértéséhez is – magyarázta Gyenge Ádám.
Forrás: Budapesti Műszaki és Gazdaságtudományi Egyetem, továbbította a Helló Sajtó! Üzleti Sajtószolgálat.Letölthető fotók
Gyenge Ádám (BME Matematikai Intézet; jobbra) és Szabó Szilárd (a kutatás idején BME, jelenleg ELTE Matematikai Intézet; balra).
Úszógumi alakú tórusz.
